- Autors admin [email protected].
- Public 2023-12-16 19:25.
- Pēdējoreiz modificēts 2025-06-01 06:13.

Zelta koeficienta piemērus var atrast visur klasiskajā arhitektūrā, mākslas darbos, dabā un pat mūzikā. Šī proporcijas izteiksme, kas pazīstama arī kā Dievišķā attiecība, piedāvā harmonisku kompozīciju, izmantojot neracionālu skaitli (1,618) dizainā, gan dabiskā, gan cilvēka radītā. Visticamāk, jūs nezināt par matemātiku, kas slēpjas Zelta koeficienta skaistumā, jo tā rada objektus un mūziku, kas jums, protams, šķitīs patīkama, bez nepieciešamības paskaidrot.
Zelta attiecība arhitektūrā
Zelta attiecība rada gandrīz ideālu skaistumu dabā un mākslā. Kad sākat meklēt Zelta koeficienta piemērus ikdienas dzīvē, jūs varat būt pārsteigts par daudzajiem gadījumiem, kad tā ir izmantota daudzu monumentālu ēku un būvju radīšanai. Kad arhitektūrā tiek izmantota Zelta attiecība, tiek uzskatīts, ka ēka ir izveidota, izmantojot "sakrālo arhitektūru". Piemērojot zelta koeficienta aprēķinu kvadrātam, arhitekti un dizaineri var izveidot Zelta taisnstūri, kuram, domājams, ir cilvēka acij estētiski vispievilcīgākās proporcijas.
Zelta taisnstūra piemērs: Partenons

Grieķu tēlnieks Fidiass savos darbos izmantoja Zelta koeficientu, it īpaši, kad viņš sāka strādāt ar lentēm, kuras viņš veidoja tieši virs Partenona kolonnām. Ir arī svarīgi atzīmēt, ka zelta koeficientam piešķirtā skaitliskā vērtība Phi tika nosaukta viņam par godu.
Ja izmērīsit Partenona ārpuses izmērus, jūs atklāsiet, ka tas ne tikai veido zelta taisnstūri, bet arī starp kolonnām ir daudz zelta taisnstūri. Šī sakrālā struktūra ir skaists arhitektūras zelta attiecības piemērs.
Zelta trīsstūra piemērs: Lielā Gīzas piramīda
Zelta attiecība, zelta taisnstūris un zelta trīsstūris ir atrodami viena no septiņiem pasaules brīnumiem - Lielās Gīzas piramīdas - pilnībā. Lai atrastu zelta attiecību, piramīdas kvadrātveida pamatne ir jāsamazina uz pusi un jānovelk vertikāla līnija piramīdas centrā. Ja tas ir savienots ar leņķisko piramīdas malu, varat viegli redzēt, kā tas veido Zelta trīsstūri ar koeficientu 1,618, Zelta koeficientu.
Citi arhitektūras piemēri
Jūs varat atrast daudzus senās līdz mūsdienu sakrālās arhitektūras piemērus un Zelta proporcijas ēkas.
- Šartras katedrāle - centrs, Francija
- Notre Dame - Parīze, Francija
- Meiteņu lievenis - Akropole, Atēnas
- Taj Mahal - Agra, Indija
- Apvienoto Nāciju Organizācijas ēka - Ņujorka, Ņujorka
Zelta attiecība mākslas piemēros
Var atrast daudzus piemērus no gleznotāju meistariem, kuri izmantoja Zelta koeficientu. Šie pilnības darbi radīti, izmantojot zelta taisnstūri un zelta trīsstūri attiecību. Māksla, kas radīta, pamatojoties uz Zelta taisnstūri, izrādās patīkamāka cilvēka acij. Tas ir viens no noslēpumiem, kas ieskauj šo ideālo taisnstūri un zelta attiecību.
Zelta attiecība mākslā

Zelta griezuma mākslas piemēri:
- Leonardo Di Vinči - Mona Liza, Vitruvian Man
- Botičelli - Veneras dzimšana
- Mikelandželo - Svētā ģimene, ' Dāvids'
- Rafaels - krustā sišana
- Rembrants - pašportrets
- Salvadors Dalī - Pēdējā vakarēdiena sakraments, Atmiņas noturība
Zelta koeficienta izmantošana mākslas kompozīcijā
Zelta taisnstūrī ir noteiktas zonas, kas ir vizuāli pievilcīgākas nekā citas zonas. Šos punktus atklāj, novelkot līniju no taisnstūra apakšējā stūra uz pretējo stūri un atkārtojot to ar otru apakšējo stūri. Šīs līnijas krustosies tieši zelta taisnstūra centrā. Pēc tam izmēriet vidusceļu pa katru līniju, sākot no centra punkta. Šos četrus punktus sauc par taisnstūra acīm (zelta attiecība). Gleznas galvenais fokusa punkts pēc tam tiek uzzīmēts vai krāsots šajos interešu punktos (attiecībās).
Zelta attiecība mūzikā

Mūzika sastāv no skaitliskām vērtībām, un, kad mūzikas skaņdarba radīšanai tiek izmantota Zelta attiecība, tā kļūst par dzīvu matemātikas piemēru. Fibonači secība ir izplatīta arī mūzikā:
- Skalā ir astoņas notis.
- Trešā un piektā nots ir akordu pamatā.
- Jebkuras nots garums jeb oktāva ir 13 notis.
Secība turpinās visā skaņdarbā un kļūst sarežģītāka, sasniedzot zelta koeficientu.
Komponisti, kuri izmantoja zelta koeficientu
Daži no pazīstamākajiem klasiskajiem komponistiem savos skaņdarbos izmantoja Zelta koeficientu un Fibonači secību, tostarp Bahs, Bēthovens, Šopēns un Mocarts. Daži mūsdienu komponisti, piemēram, Keisijs Mongovens, savā mūzikā ir izpētījuši Zelta attiecību.
Zelta koeficienta piemēri dabā

Kur dabā ir atrodama Zelta attiecība? Tas atrodas zelta vai Fibonači spirālē, ko var izveidot, izmantojot zelta attiecību. Šī ir parādība, kas plaši sastopama dabiskajā pasaulē. Auga lapas aug tā, lai pēc iespējas vairāk varētu virzīties pa stublāju uz augšu. Jauna lapa veidojas tikai pēc tam, kad tā ir izveidojusies.
- Spirālveida kaktusi
- Spirālveida galaktikas
- Saulespuķes
Ziedi ar Fibonači secību
Dažiem ziediem ir ziedu ziedlapiņas, kas atbilst Fibonači secībai:
- Trīs ziedlapiņas:Īrisa, lilija, orhidejas, trilijs
- Piecas ziedlapiņas: Buttercups, pelargonijas, hibisks, rīta krāšņums, nasturcija
- Astoņas ziedlapiņas: Delphiniums
- 13 ziedlapiņas: Atsevišķas margrietiņu šķirnes, ambrozijas, kliņģerītes
Fibonači spirāle priežu čiekuros

Atkarībā no koku sugas, jūs varat redzēt arī Zelta koeficientu, kas darbojas Fibonači skaitļu sērijā priežu čiekuros. Vienā priedes čiekura pusē var atrast astoņu spirāļu sēriju, bet otrā pusē ir 13 spirāles. Citam priežu čiekuru rakstam ir piecas spirāles vienā pusē un astoņas otrā pusē.
Zelta attiecība cilvēkos
Šī attiecība ir svarīga arī ne tikai tam, kā cilvēki uztver viens otru, bet arī to, kā darbojas viņu ķermenis un DNS.
DNS atklāj zelta attiecību
Viens no pārsteidzošākajiem Zelta koeficienta piemēriem ir atrodams cilvēka DNS struktūrā. To var redzēt vienā DNS šķērsgriezumā, kas atklāj, ka DNS dubultā spirāle veido desmitstūra formu. Tā ir divu piecstūru kombinācija, kas pagriezti par 36 grādiem viens no otra, veido DNS dubulto spirāli. Pati dubultspirāle veido piecstūri. Pat viena DNS molekula atklāj zelta griezuma jeb dievišķās proporcijas pamatu.
Math Behind the Golden Ratio
Zelta koeficienta atrašana reālajā dzīvē ir vienkārša, jo tā parādās visapkārt. Tas ir matemātisks patiesība, ko izmanto, lai definētu to, kas parasti tiek dēvēts par ideālo dabā sastopamo skaitli, ko cilvēki ir dublējuši un atdarinājuši gadsimtiem ilgi. Šī numura vienkāršotais skaistums slēpj tā izpildes sarežģītību. Lai saprastu teoriju par zelta koeficientu, vispirms ir jāizpēta Fibonači koeficienta secība.
Fibonači secība un zelta attiecība
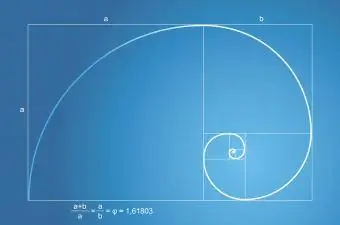
Fibonači secībai vai sērijai ir saistība ar zelta koeficientu. Fibonači sērija parādās kā lapu skaits uz auga un ziedlapu skaits uz zieda. Dabā sastopamā Fibonači spirāle vienmēr ir daļa no zelta taisnstūra ar zelta attiecību.
Fibonači sērijas matemātika ir vienkārša:
- Secība sākas ar 0 un 1.
- Vienkārši pievienojiet pēdējos divus skaitļus, lai iegūtu nākamo sērijas numuru.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8 un tā tālāk.
- Šis Fibonači sērijas piemērs ir šāds: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 un tā tālāk.
Fibonači saistība ar Zelta koeficientu tiek realizēta, kad to pievieno uz priekšu, tālāk un tālāk. Jo vairāk jūs pievienojat sēriju, jo tuvāk jūs nonāksit Zelta koeficientam.
Zelta taisnstūra un trīsstūra izveide
Lai izveidotu zelta taisnstūri ar Fibonači secību, sāciet ar kvadrātu. Jūs sāksit veidot taisnstūri, pievienojot sākotnējam kvadrātam vēl vienu kvadrātu. Atcerieties izmantot formulu: 0+1=1 ir pirmais kvadrāts, 1+1=2 - jūs pievienosit vēl vienu kvadrātu.1+2=3 pievienosit trīs kvadrātus, un pēc tam, 2+3=5, pievienosit piecus kvadrātus. Jūs turpināsit pievienot kvadrātus un galu galā izveidot zelta taisnstūri.
Zelta trīsstūri var izveidot, sadalot zelta taisnstūri uz pusēm no viena stūra uz pretējo stūri. Tādējādi tiek izveidots trīsstūris, kura trīs malu vai leņķu attiecība ir 2:2:1, kas nozīmē, ka abas garās malas ir vienādas garumā un īsais leņķis ir tieši puse no divu garāko malu garuma.
Zelta koeficients reālajā pasaulē
Zelta attiecību bieži dēvē par dievišķo attiecību, jo tā ir ievērojama dabā un cilvēka ķermenī. Atklājums, ka zelta attiecība ir klātesoša tik daudzās dzīvās būtnēs, veicināja godbijību pret šo maģisko proporciju, un tas joprojām ir iedvesmas avots māksliniekiem un radītājiem arī mūsdienās.






